Addition des vecteurs
Exercice 1 : Égalités vectorielles
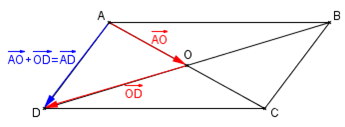
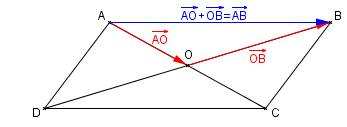
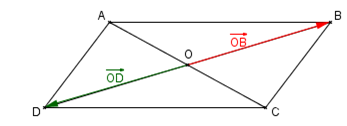
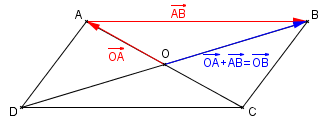
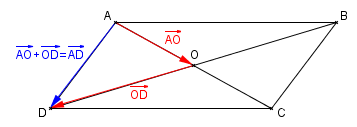
Soit ABCD un parallélogramme de centre O. Compléter les égalités vectorielles suivantes :
- $\overrightarrow{AO}+\overrightarrow{OD}=...$
- $\overrightarrow{OB}+\overrightarrow{AO}=...$
- $\overrightarrow{OB}+\overrightarrow{OD}=...$
- $\overrightarrow{OA}+\overrightarrow{AB}=...$
- $\overrightarrow{CD}+\overrightarrow{CB}=...$
Exercice 2 : Pavage
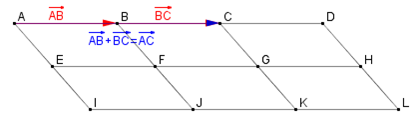
On a construit un pavage de parallélogrammes identiques. Compléter les égalités suivantes :
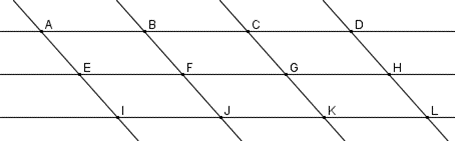
- $\overrightarrow{AB}+\overrightarrow{BC}=...$
- $\overrightarrow{AB}+\overrightarrow{AE}=...$
- $\overrightarrow{AF}+\overrightarrow{AG}=...$
- $\overrightarrow{FH}+\overrightarrow{CE}=...$
- $\overrightarrow{AF}+\overrightarrow{GJ}=...$
- $\overrightarrow{AF}+\overrightarrow{IG}=...$
Exercice 3 : Centre de gravité
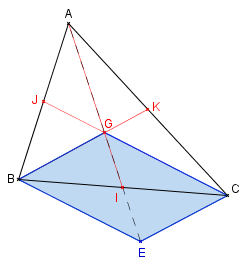
- Construire un triangle ABC, son centre de gravité G, et le point E, symétrique de A par rapport à G.
- Démontrer que le quadrilatère BGCE est un parallélogramme.
- Que peut-on en déduire pour $\overrightarrow{GB}+\overrightarrow{GC}$ ?
- Démontrer que $\overrightarrow{GA}+\overrightarrow{GB}+\overrightarrow{GC}=\vec{0}$.
Exercice 4 : Hexagone régulier
Soit ABCDEF un hexagone régulier de centre O. Compléter les égalités vectorielles en utilisant les points de la figure.
- $\overrightarrow{AB}+\overrightarrow{BC}=...$
- $\overrightarrow{AB}+\overrightarrow{AO}=...$
- $\overrightarrow{AB}+\overrightarrow{CD}=...$
- $\overrightarrow{OE}+\overrightarrow{OC}=...$
Exercice 5 : Sommes sur une figure
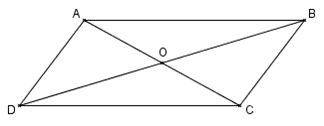
En utilisant la figure ci-dessous où ABCD est un parallélogramme, simplifier les sommes vectorielles suivantes.
- $\overrightarrow{AB}+\overrightarrow{BC}=...$
- $\overrightarrow{DA}+\overrightarrow{DC}=...$
- $\overrightarrow{AD}+\overrightarrow{CB}=...$
- $\overrightarrow{AB}+\overrightarrow{AD}=...$