Vecteurs dans un repère
Exercice 1 : Nature d'un parallélogramme
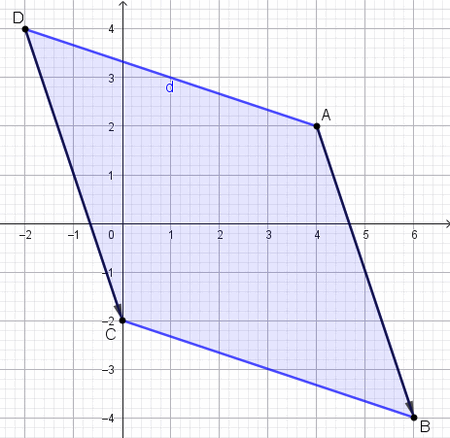
Dans un repère orthonormé (O, I, J), on donne les points $A(4;2)$, $B(6;-4)$ et $C(0;-2)$.
- Placer les points.
- Déterminer les coordonnées du vecteur $\overrightarrow{AB}$.
- En déduire les coordonnées du point D pour que le quadrilatère ABCD soit un parallélogramme.
- Calculer les longueurs AB et BC. En déduire la nature du parallélogramme ABCD.
Exercice 2 : Coordonnées dans un repère
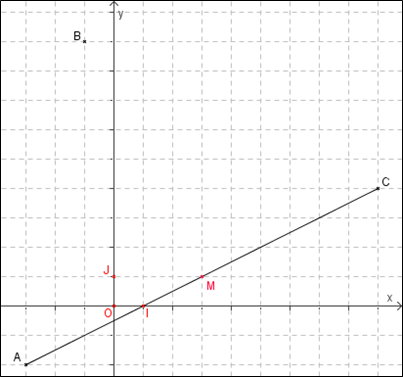
Dans un repère orthonormé, on considère les points $A(-3;-2)$, $B(-1;9)$ et $C(9;4)$.
- Faire une figure.
- On note M le milieu du segment [AC]. Calculer les coordonnées de M.
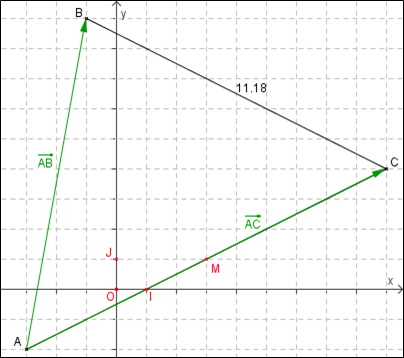
- Calculer les coordonnées des vecteurs $\overrightarrow{AB}$ et $\overrightarrow{AC}$.
- Calculer la longueur BC (valeur arrondie à 0,1 près).
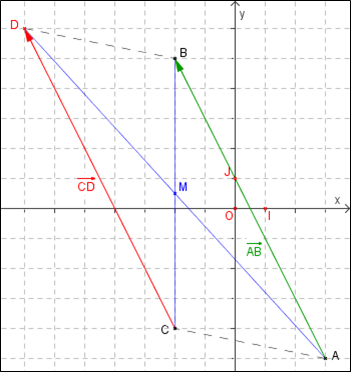
Exercice 3 : Translation
Le plan est muni d'un repère orthonormé.
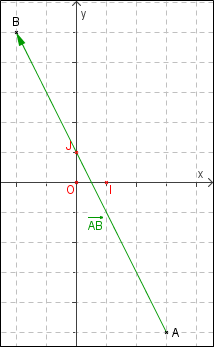
- Placer les points $A(3;-5)$ et $B(-2;5)$. Donner les coordonnées du vecteur $\overrightarrow{AB}$ et calculer la longueur AB.
- Placer le point $C(-2;-4)$. Construire le point D, image de C par la translation de vecteur $\overrightarrow{AB}$.
- Quelles sont les coordonnées de D ?
- Quelle est la nature du quadrilatère ABDC ? Quelles sont les coordonnées du point M, intersection de ses diagonales ?