Transformations du plan
Exercice 1 : Translations
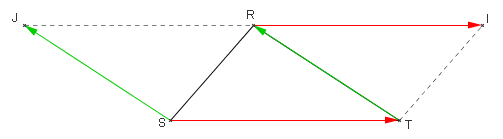
On considère le triangle RST.
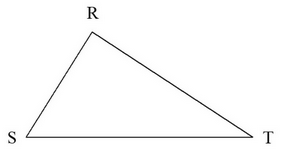
- Construire I, image de R par la translation de vecteur $\overrightarrow{ST}$.
- Construire J, image de S par la translation de vecteur $\overrightarrow{TR}$.
- Démontrer que R est le milieu du segment [IJ].
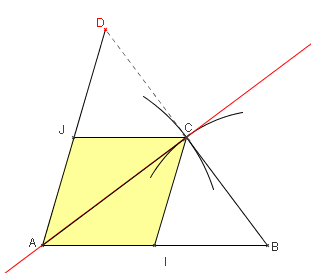
Exercice 2 : Losange et symétrie
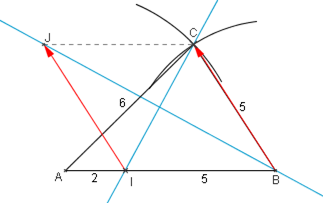
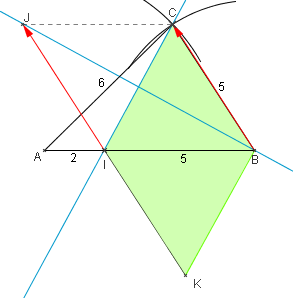
- Construire un triangle ABC tel que $AB=7$ cm, $AC=6$ cm et $BC=5$ cm. On appelle I le point de [AB] tel que $AI=2$ cm.
- Construire J, image de I par la translation de vecteur $\overrightarrow{BC}$. Démontrer que (BJ) et (CI) sont perpendiculaires.
- Construire K, image de J par la symétrie de centre I. Quelle est la nature du quadrilatère BCIK ?
Exercice 3 : Symétrie axiale et losange
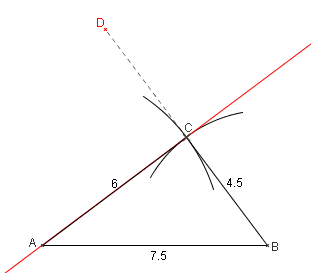
- Construire un triangle ABC tel que $AB=7,5$ cm, $AC=6$ cm et $BC=4.5$ cm.
- Démontrer que le triangle ABC est rectangle en C.
- On appelle I et J les milieux de [AB] et [AD], où D est le symétrique de B par rapport à (AC). Démontrer que AICJ est un losange.
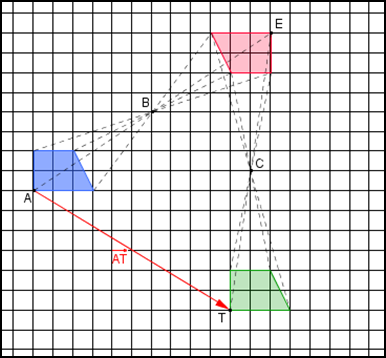
Exercice 4 : Composition de symétries
- Sur la figure, construire la figure $\mathcal{F}_{1}$, image de $\mathcal{F}$ par la symétrie centrale de centre B.
- Construire la figure $\mathcal{F}_{2}$, image de $\mathcal{F}_{1}$ par la symétrie centrale de centre C.
- Quelle transformation permet de passer directement de la figure $\mathcal{F}$ à la figure $\mathcal{F}_{2}$ ?