Vecteurs du plan
Exercice 1 : Milieux et vecteurs
On considère la figure ci-dessous où I, J et K sont les milieux respectifs de [BC], [AC] et [AB].
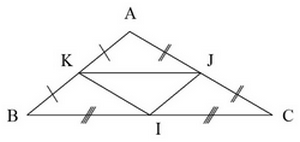
- Démontrer que $\overrightarrow{AK}=\overrightarrow{KB}$.
- Quelle est la nature du quadrilatère BIJK?
- En déduire 2 doubles égalités vectorielles.
Exercice 2 : Construction et vecteurs
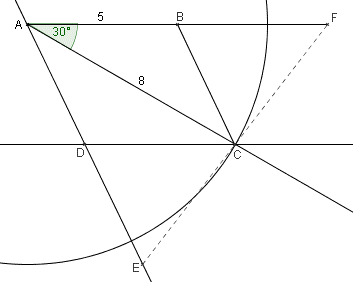
- Construire un parallélogramme ABCD tel que $AB=5$ cm, $AC=8$ cm et $\widehat{BAC}=30^{\circ}$.
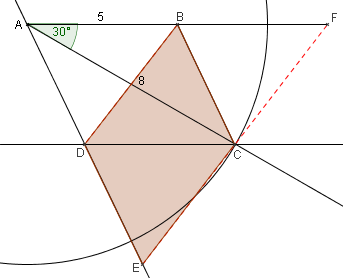
- Construire les points E et F tels que $\overrightarrow{DE}=\overrightarrow{AD}$ et $\overrightarrow{BF}=\overrightarrow{AB}$.
- Démontrer que $\overrightarrow{EC}=\overrightarrow{CF}$.
Exercice 3 : Diagonales
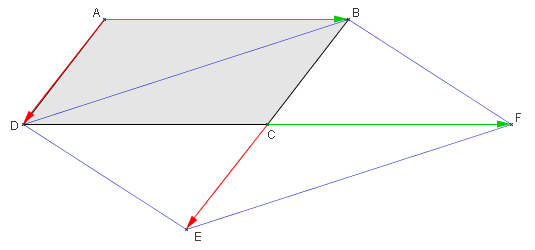
- Construire un parallélogramme ABCD, puis les points E et F tels que $\overrightarrow{CE}=\overrightarrow{AD}$ et $\overrightarrow{CF}=\overrightarrow{AB}$.
- Démontrer que le quadrilatère BFED est un parallélogramme.
Exercice 4 : Milieux multiples
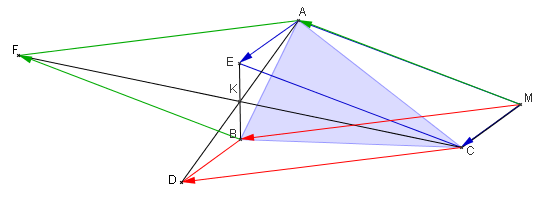
Soit ABC un triangle et M un point quelconque.
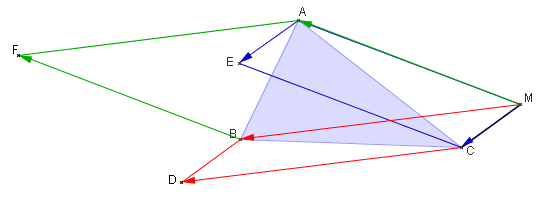
- Construire D, E et F tels que MBDC, MCEA et MAFB soient des parallélogrammes.
- Démontrer que $\overrightarrow{AE}=\overrightarrow{BD}$ et en déduire que [AD] et [BE] ont le même milieu.
- Démontrer que [AD], [BE] et [CF] ont le même milieu.