Coordonnées, distances et milieux
Exercice 1 : Triangle isocèle ?
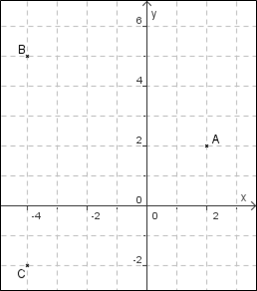
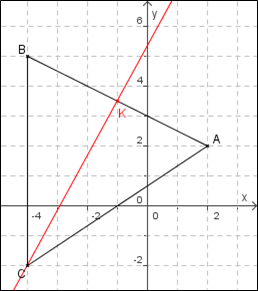
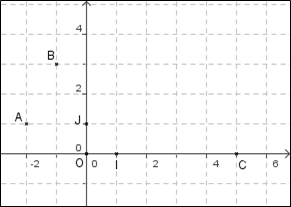
- Dans un repère orthonormé, placer les points $A(2;2)$, $B(-4;5)$ et $C(-4;-2)$.
- Montrer que $AC = \sqrt{52}$ cm.
- Calculer BC. Le triangle ABC est-il isocèle en C ?
- Construire K, milieu de [AB]. La droite (CK) est-elle la médiatrice de [AB] ? Justifier.
Exercice 2 : Triangle isocèle et aire
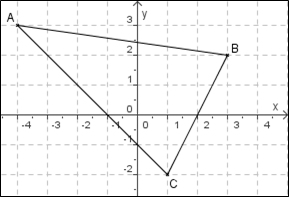
Dans un repère orthonormé, on considère les points $A(-4;3)$, $B(3;2)$ et $C(1;-2)$.
- Calculer AB. On admet que $AC=\sqrt{50}$ et $BC=\sqrt{20}$. Que peut-on en déduire pour le triangle ABC ?
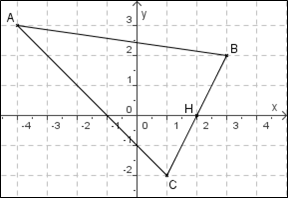
- Soit H le milieu de [BC]. Vérifier par le calcul que H a pour coordonnées (2;0).
- Pourquoi le segment [AH] est-il une hauteur du triangle ABC ?
- Prouver que $AH=3\sqrt{5}$ et calculer l'aire du triangle ABC.
Exercice 3 : Triangle rectangle et rectangle
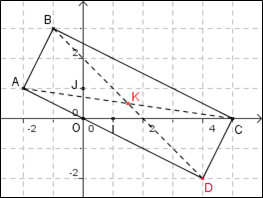
On considère les points $A(-2;1)$, $B(-1;3)$ et $C(5;0)$.
- Démontrer que $AB = \sqrt{5}$.
- On admet que $AC=5\sqrt{2}$ et $BC=3\sqrt{5}$. Démontrer que le triangle ABC est rectangle en B.
- Calculer les coordonnées de K, milieu de [AC].
- On appelle D le point tel que ABCD soit un rectangle. Calculer ses coordonnées.
Exercice 4 : Parallélogramme ou rectangle ?
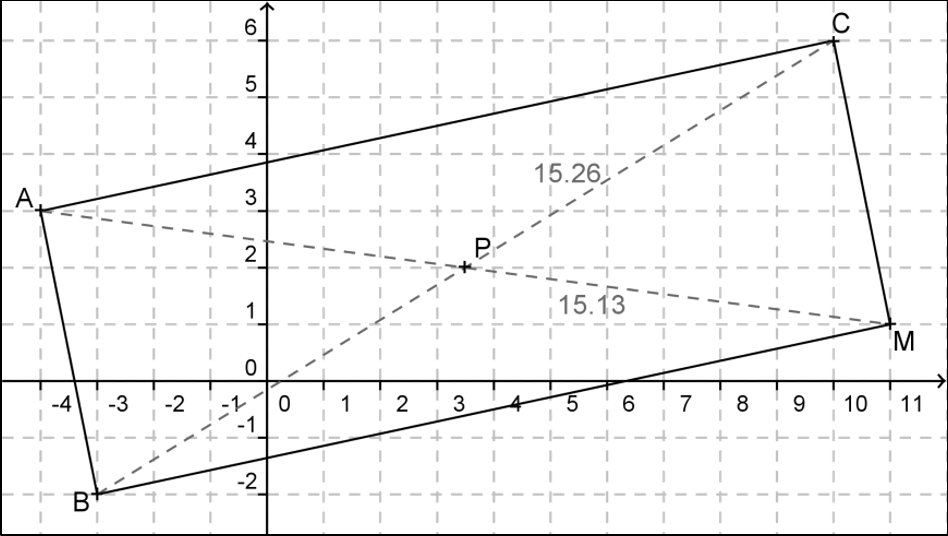
On donne les points $A(-4;3)$, $B(-3;-2)$ et $C(10;6)$.
- Calculer les coordonnées du point M tel que ABMC soit un parallélogramme.
- ABMC est-il un rectangle ? Justifier.
Exercice 5 : Nature d'un quadrilatère
On donne les points $A(5;3)$, $B(2;-3)$ et $C(-2;-1)$.
- Quelle est la nature du triangle ABC ?
- Calculer les coordonnées du point D tel que ACBD soit un parallélogramme.
- Quelle est la nature du quadrilatère BCMA (M est défini dans le corrigé) ?
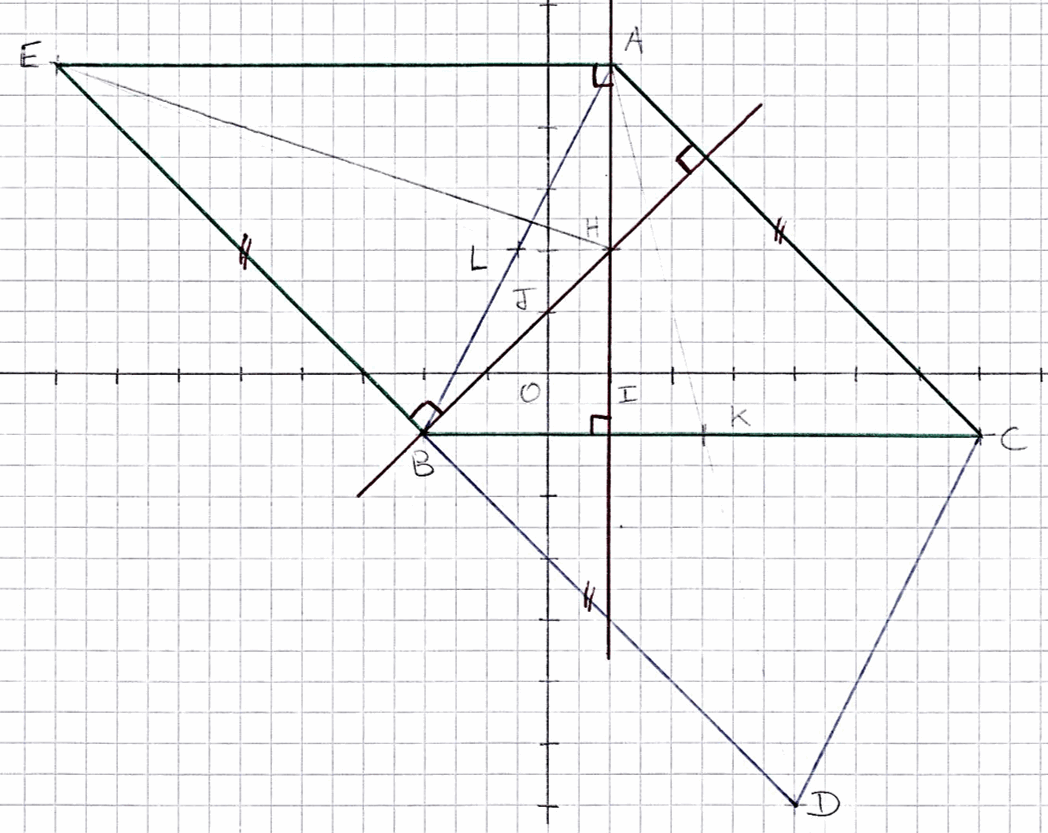
Exercice 6 : Orthocentre
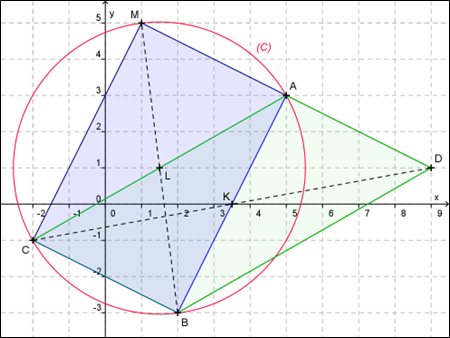
On considère les points $A(1;5)$, $B(-2;-1)$, $C(7;-1)$ et $H(1;2)$.
- Déterminer les coordonnées des points D et E tels que ABDC et ACBE soient des parallélogrammes.
- Montrer que le triangle HBE est rectangle en B.
- Montrer que la droite (HB) est la médiatrice du segment [ED].
- Que représente le point H pour le triangle ABC ?
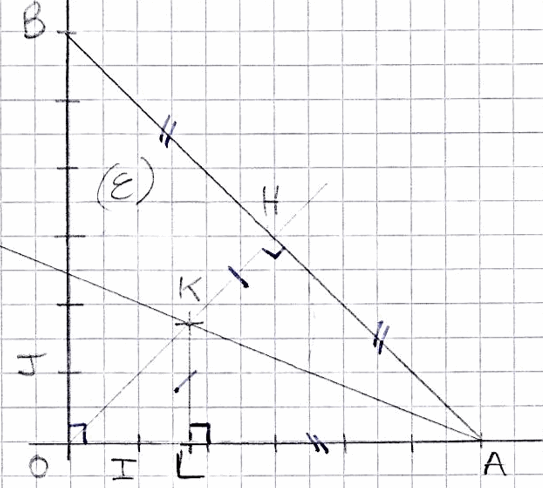
Exercice 7 : Centre du cercle inscrit
On considère les points $A(6;0)$ et $B(0;6)$ dans un repère orthonormé (O,I,J).
Démontrer que le point $K(6-3\sqrt{2}; 6-3\sqrt{2})$ est le centre du cercle inscrit dans le triangle OAB.