Rappels en géométrie de collège
Exercice 1 : Triangle rectangle et symétrie
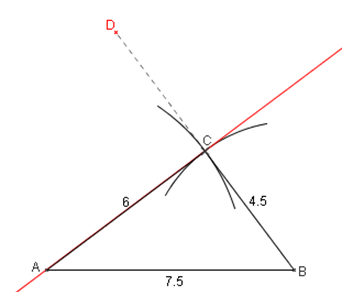
- Construire un triangle ABC tel que $AB=7,5$ cm, $AC=6$ cm et $BC=4,5$ cm.
- Construire le point D, image du point B par la symétrie d'axe (AC).
- Démontrer que le triangle ABC est rectangle en C.
- Démontrer que C est le milieu du segment [BD].
Exercice 2 : Aire et hauteur
Le triangle BUC est rectangle en U. On donne $BU=16$ et $BC=20$. La hauteur issue de U coupe (BC) en H.
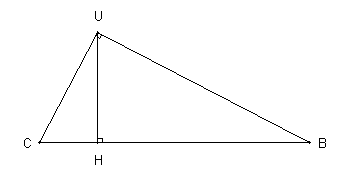
- Calculer la longueur UC.
- Calculer l'aire du triangle BUC, puis en déduire la longueur UH.
Exercice 3 : Angles et Pythagore
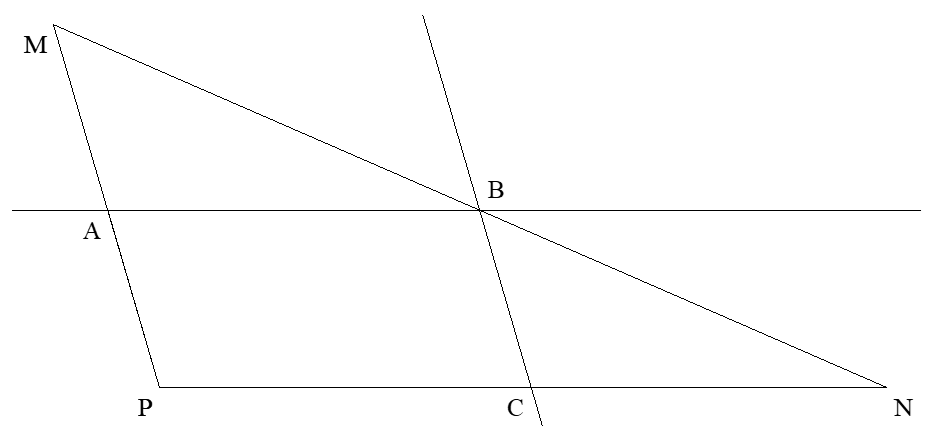
Dans la figure ci-contre, on sait que le triangle NEP est isocèle en N, $\hat{NMP}=35^\circ$, $\hat{NEP}=55^\circ$, $MN=9$ et $MP=10$.
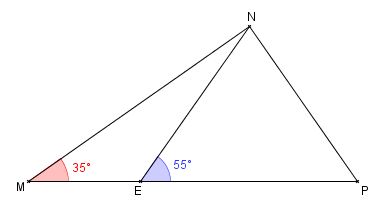
Calculer la longueur NP arrondie au dixième.
Exercice 4 : Médiatrice et parallélogramme
Sur la figure ci-contre, on a $BE=6$ cm, $EF=4,5$ cm et $AC=7,5$ cm. La droite (d) est la médiatrice du segment [AE] et BEFC est un parallélogramme.
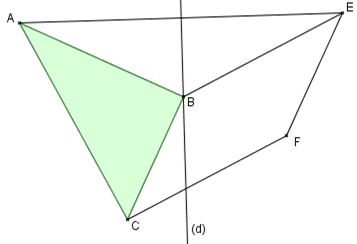
Démontrer que le triangle ABC est rectangle.
Exercice 5 : Symétries et médiatrice
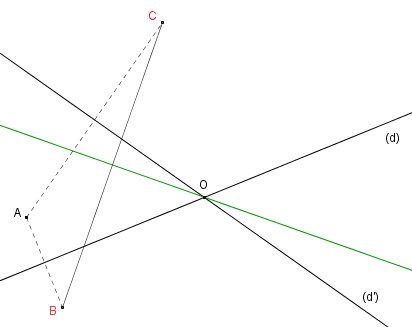
On considère deux droites (d) et (d') sécantes en O, et un point A n'appartenant à aucune des deux droites. On appelle B le symétrique de A par rapport à (d) et C le symétrique de A par rapport à (d').
- Faire une figure.
- Démontrer que O appartient à la médiatrice du segment [BC].
Exercice 6 : Symétrie et bissectrice
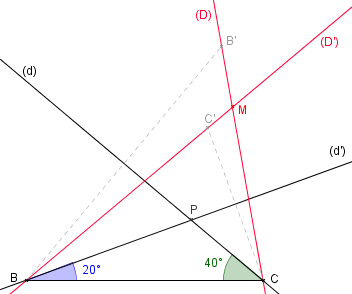
On considère la figure ci-contre.
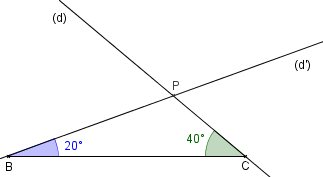
- Reproduire la figure, puis construire la droite (D) symétrique de (BC) par rapport à (d), et (D') symétrique de (BC) par rapport à (d'). Les droites (D) et (D') se coupent en M.
- Démontrer que (MP) est la bissectrice de l'angle $\hat{BMC}$.
Exercice 7 : Thalès et parallélogramme
Le triangle MNP est tel que $MP=8$ cm, $PN=12$ cm et $MN=15$ cm. Le point A est sur [MP] tel que $PA=4,8$ cm. La parallèle à (PN) passant par A coupe (MN) en B. La parallèle à (MP) passant par B coupe (NP) en C.
- Faire la figure.
- Démontrer que le quadrilatère ABCP est un parallélogramme.
- Calculer AB.
- Préciser la nature du parallélogramme ABCP.
Exercice 8 : Cercle et trigonométrie
Tracer un cercle (C) de centre O et de rayon 4 cm. Placer A et B tels que [AB] soit un diamètre. Placer un point E sur (C) tel que $\hat{BAE}=40^{\circ}$.
- Montrer que le triangle ABE est rectangle.
- Calculer la valeur exacte de BE puis son arrondi au millimètre.
- Placer D, symétrique de B par rapport à E. Démontrer que (AD) // (OE).
- Quelle est la nature du triangle ABD ? Justifier.