Évaluation de MATHÉMATIQUES
Niveau Première - La Dérivation
Exercice 1 : Calculs de dérivées (4,5 pts)
Pour chaque fonction, donner son domaine de définition et donner l'expression de sa fonction dérivée sous la forme la plus simple possible.
- $f(x) = x^{4} + 2x^{3} - x - \dfrac{1}{x}$
- $g(x) = \left( -x^{2} + 1 \right)\sqrt{x}$
- $h(x) = \dfrac{2 - x}{\sqrt{x}}$
1. Fonction $f$ :
La fonction est définie pour $x \neq 0$, donc $\mathcal{D}_f = \mathbb{R}^*$.
$f'(x) = 4x^3 + 2 \times 3x^2 - 1 - \left( -\dfrac{1}{x^2} \right) = $ $4x^3 + 6x^2 - 1 + \dfrac{1}{x^2}$.
2. Fonction $g$ :
La fonction est définie pour $x \ge 0$, donc $\mathcal{D}_g = [0 ; +\infty[$.
On utilise $(uv)' = u'v + uv'$ avec $u(x) = -x^2+1$ et $v(x) = \sqrt{x}$.
$g'(x) = -2x\sqrt{x} + (-x^2+1)\dfrac{1}{2\sqrt{x}} = \dfrac{-4x^2 - x^2 + 1}{2\sqrt{x}}$.
Donc $g'(x) = \dfrac{-5x^2 + 1}{2\sqrt{x}}$.
3. Fonction $h$ :
La fonction est définie pour $x > 0$, donc $\mathcal{D}_h = ]0 ; +\infty[$.
On utilise $\left( \dfrac{u}{v} \right)' = \dfrac{u'v - uv'}{v^2}$.
$h'(x) = \dfrac{-1\sqrt{x} - (2-x)\dfrac{1}{2\sqrt{x}}}{(\sqrt{x})^2} = $ $\dfrac{-x - 2}{2x\sqrt{x}}$.
Exercice 2 : Nombre dérivé et tangente (5 pts)
Soit $f$ la fonction définie sur $\mathbb{R}$ par $f(x) = \dfrac{x}{x^{2} + 1}$.
- Déterminer $\dfrac{f(h) - f(0)}{h}$ en fonction de $h$ sous la forme la plus simple possible.
- En déduire que $f$ est dérivable en $0$ et donner la valeur de $f'(0)$.
- Donner une équation de la tangente à la courbe représentative de $f$ au point d'abscisse $0$.
- Donner l'expression de la fonction dérivée $f'$ de $f$, puis vérifier l'exactitude du résultat obtenu à la question 2.
1. Taux d'accroissement :
$f(0) = 0$.
$\dfrac{f(h) - f(0)}{h} = \dfrac{\dfrac{h}{h^2+1}}{h} = $ $\dfrac{1}{h^2+1}$.
2. Dérivabilité :
$\lim\limits_{h \to 0} \dfrac{1}{h^2+1} = 1$.
$f$ est dérivable en $0$ et $f'(0) = 1$.
3. Équation de la tangente :
$y = f'(0)(x - 0) + f(0)$, soit $y = x$.
4. Fonction dérivée :
$f'(x) = \dfrac{1(x^2+1) - x(2x)}{(x^2+1)^2} = $ $\dfrac{1 - x^2}{(x^2+1)^2}$.
On a bien $f'(0) = \dfrac{1-0}{(0+1)^2} = 1$.
Exercice 3 : Lecture graphique (5,5 pts)
On a représenté la courbe $C_f$ d'une fonction $f$ définie sur $[-11 ; 6]$. On a tracé trois tangentes : $(AG)$, $(EB)$ et $(EC)$.
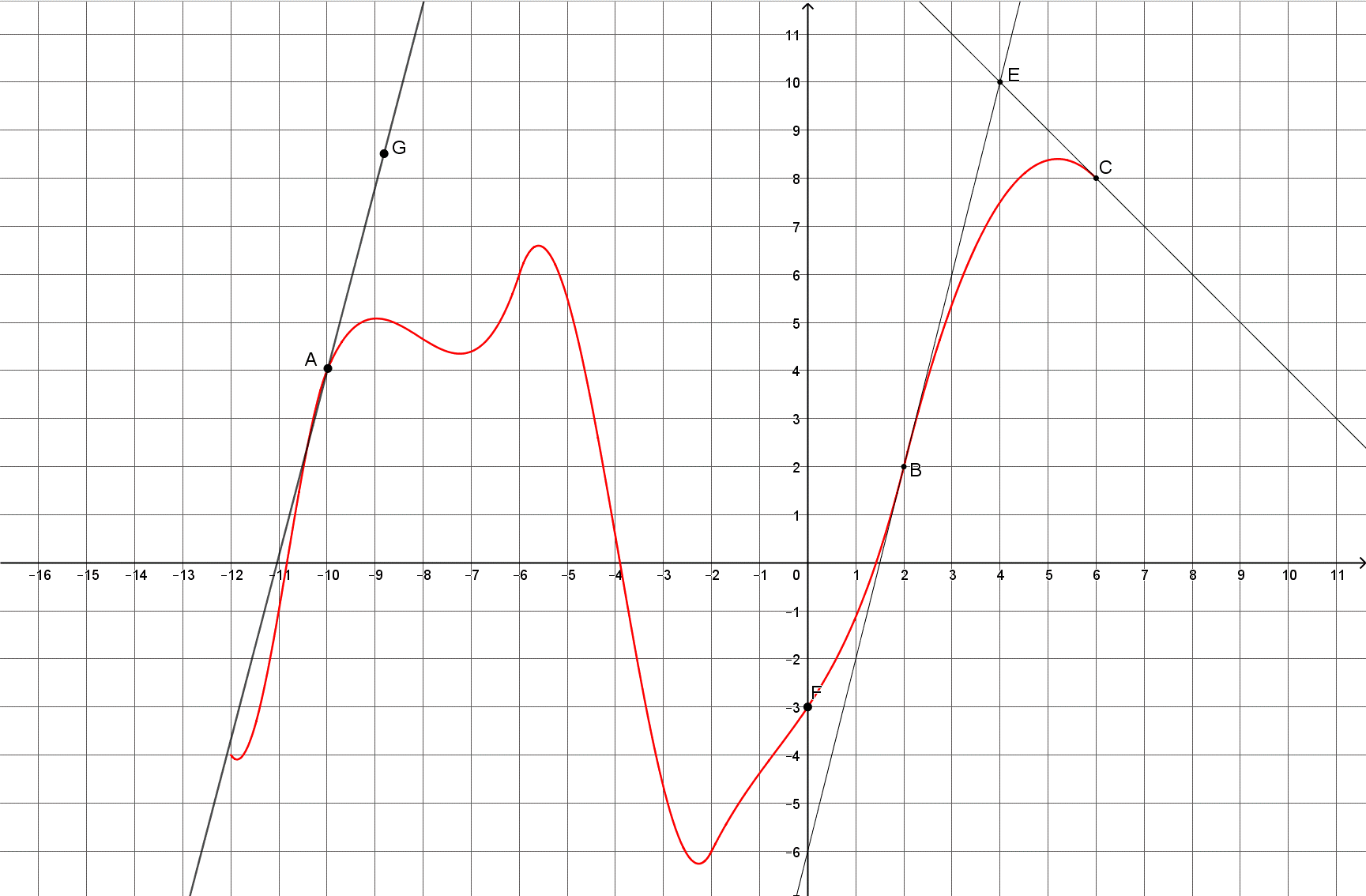
- Donner les équations réduites des droites $(EB)$ et $(EC)$ avec $B(2 ; 2)$, $E(4 ; 10)$ et $C(6 ; 8)$.
- En déduire les valeurs de $f'(2)$ et $f'(6)$.
- Sachant que $f'(-10) = \dfrac{9}{2}$, déterminer l'équation de la droite $(AG)$ passant par $A(-10 ; 4)$.
1. Équations réduites des droites $(EB)$ et $(EC)$ :
La forme générale d'une équation de droite est $y = mx + p$.
$\bullet$ Pour la droite $(EB)$ : Elle passe par $B(2 ; 2)$ et $E(4 ; 10)$.
Calcul du coefficient directeur $m$ :
$m = \dfrac{y_E - y_B}{x_E - x_B} = \dfrac{10 - 2}{4 - 2} = \dfrac{8}{2} = 4$.
Calcul de l'ordonnée à l'origine $p$ :
L'équation est de la forme $y = 4x + p$. Le point $B(2 ; 2)$ appartient à la droite :
$2 = 4 \times 2 + p \iff 2 = 8 + p \iff p = -6$.
L'équation réduite de $(EB)$ est donc $y = 4x - 6$.
$\bullet$ Pour la droite $(EC)$ : Elle passe par $E(4 ; 10)$ et $C(6 ; 8)$.
Calcul du coefficient directeur $m$ :
$m = \dfrac{y_C - y_E}{x_C - x_E} = \dfrac{8 - 10}{6 - 4} = \dfrac{-2}{2} = -1$.
Calcul de l'ordonnée à l'origine $p$ :
L'équation est de la forme $y = -x + p$. Le point $C(6 ; 8)$ appartient à la droite :
$8 = -1 \times 6 + p \iff 8 = -6 + p \iff p = 14$.
L'équation réduite de $(EC)$ est donc $y = -x + 14$.
2. Nombres dérivés $f'(2)$ et $f'(6)$ :
Le nombre dérivé $f'(a)$ correspond géométriquement au coefficient directeur de la tangente au point d'abscisse $a$.
$\bullet$ La droite $(EB)$ est tangente à la courbe au point $B$ d'abscisse $2$. Donc $f'(2)$ est égal au coefficient directeur de $(EB)$.
D'après la question précédente, $f'(2) = 4$.
$\bullet$ La droite $(EC)$ est tangente à la courbe au point $C$ d'abscisse $6$. Donc $f'(6)$ est égal au coefficient directeur de $(EC)$.
D'après la question précédente, $f'(6) = -1$.
3. Équation de la tangente $(AG)$ :
La formule de l'équation de la tangente au point d'abscisse $a$ est : $y = f'(a)(x - a) + f(a)$.
Ici, nous cherchons la tangente au point $A$ d'abscisse $a = -10$.
$\bullet$ On nous donne $f'(-10) = \dfrac{9}{2}$.
$\bullet$ Le point $A(-10 ; 4)$ appartient à la courbe, donc $f(-10) = 4$.
En remplaçant dans la formule :
$y = \dfrac{9}{2}(x - (-10)) + 4$
$y = \dfrac{9}{2}(x + 10) + 4$
On développe :
$y = \dfrac{9}{2}x + \dfrac{90}{2} + 4$
$y = \dfrac{9}{2}x + 45 + 4$
Finalement : $y = \dfrac{9}{2}x + 49$.
Exercice 4 : Recherche de coefficients (5 pts)
On a tracé ci-contre la courbe $C_f$ d'une fonction $f$ définie par $f(x) = ax^{2} + bx + c$. La droite $(AB)$ est tangente à $C_f$ au point $A$.
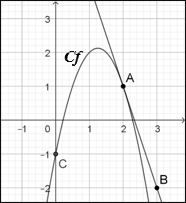
- Déterminer $c$ sachant que la courbe passe par $C(0 ; -1)$.
- À l'aide du point $A(2 ; 1)$, trouver une relation entre $a$ et $b$.
- À l'aide de la tangente $(AB)$ avec $B(3 ; -2)$, trouver une deuxième relation entre $a$ et $b$.
- En déduire l'expression de $f(x)$.
1. Valeur de $c$ : $f(0) = -1 \implies$ $c = -1$.
2. Relation 1 : $f(2) = 1 \implies 4a + 2b - 1 = 1 \implies$ $2a + b = 1$.
3. Relation 2 : $f'(2) = \dfrac{-2 - 1}{3 - 2} = -3$. Donc $4a + b = -3$.
4. Résolution : En soustrayant : $2a = -4 \implies a = -2$ donc $b = 5$.
$f(x) = -2x^2 + 5x - 1$.
